数组排序
数组排序
 数据结构和算法动态可视化 (opens new window)
数据结构和算法动态可视化 (opens new window)
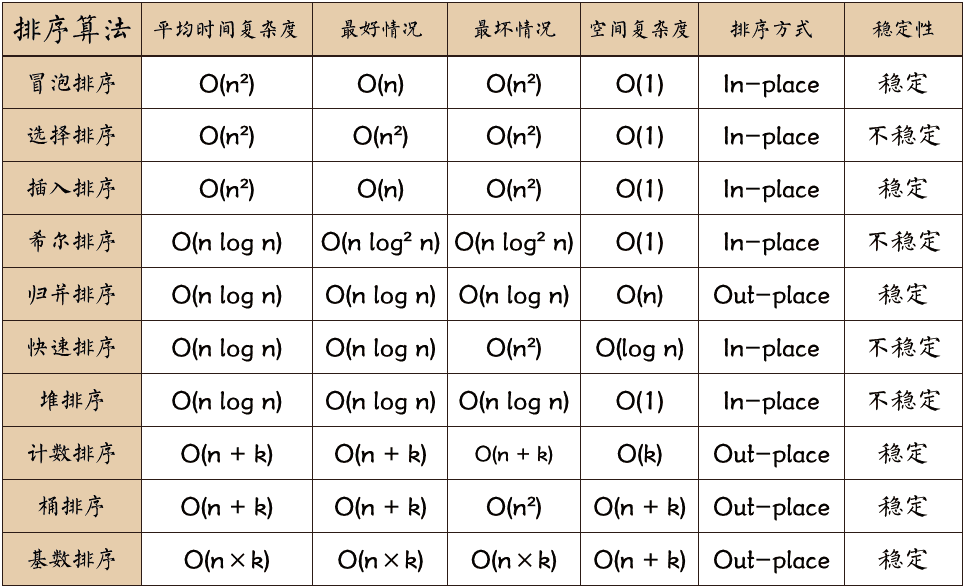
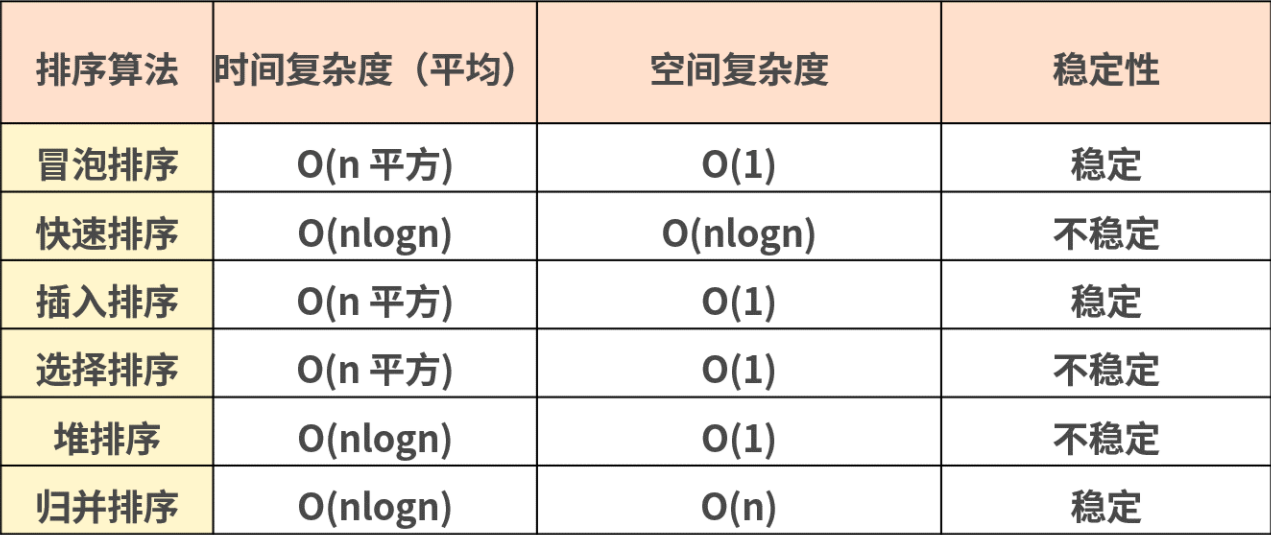
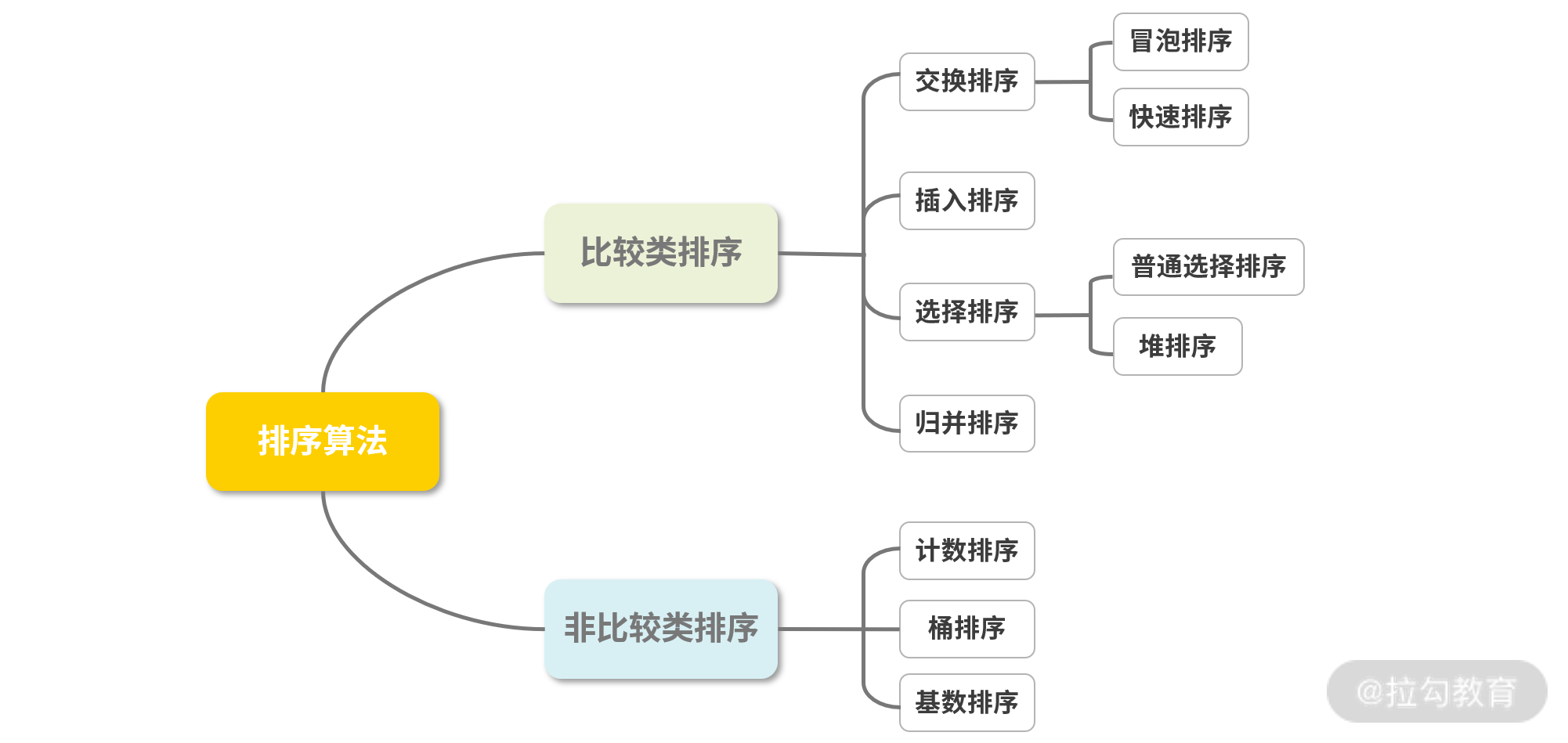
比较类排序:通过比较来决定元素间的相对次序,其时间复杂度不能突破 O(nlogn),因此也称为非线性时间比较类排序。
非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。
# 冒泡排序
冒泡排序是一次比较两个元素,如果顺序是错误的就把它们交换过来
var a = [1, 3, 6, 3, 23, 76, 1, 34, 222, 6, 456, 221];
function bubbleSort(array) {
const len = array.length;
if (len < 2) return array;
for (let i = 0; i < len; i++) {
for (let j = 0; j < i; j++) {
if (array[j] > array[i]) {
const temp = array[j];
array[j] = array[i];
array[i] = temp;
}
}
}
return array;
}
bubbleSort(a); // [1, 1, 3, 3, 6, 6, 23, 34, 76, 221, 222, 456]
# 快速排序
快速排序的基本思想是通过一趟排序,将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可以分别对这两部分记录继续进行排序,以达到整个序列有序
最主要的思路是从数列中挑出一个元素,称为 “基准”(pivot);然后重新排序数列,所有元素比基准值小的摆放在基准前面、比基准值大的摆在基准的后面;在这个区分搞定之后,该基准就处于数列的中间位置;然后把小于基准值元素的子数列(left)和大于基准值元素的子数列(right)递归地调用 quick 方法排序完成,这就是快排的思路
var a = [1, 3, 6, 3, 23, 76, 1, 34, 222, 6, 456, 221];
function quickSort(array) {
var quick = function(arr) {
if (arr.length <= 1) return arr;
const index = Math.floor(arr.length >> 1); // 相当于除以2
const pivot = arr.splice(index, 1)[0];
const left = [];
const right = [];
for (let i = 0; i < arr.length; i++) {
if (arr[i] > pivot) {
right.push(arr[i]);
} else if (arr[i] <= pivot) {
left.push(arr[i]);
}
}
return quick(left).concat([pivot], quick(right));
};
const result = quick(array);
return result;
}
quickSort(a); // [1, 1, 3, 3, 6, 6, 23, 34, 76, 221, 222, 456]
# 插入排序
构建有序数列,对于没有排序的数据,在已排序序列中从后向前扫描,找到相应位置并插入
var a = [1, 3, 6, 3, 23, 76, 1, 34, 222, 6, 456, 221];
function insertSort(array) {
const len = array.length;
let current;
let prev;
for (let i = 1; i < len; i++) {
current = array[i];
prev = i - 1;
while (prev >= 0 && array[prev] > current) {
array[prev + 1] = array[prev];
prev--;
}
array[prev + 1] = current;
}
return array;
}
insertSort(a); // [1, 1, 3, 3, 6, 6, 23, 34, 76, 221, 222, 456]
自己简化的
function insertSort(array) {
for (let i = 1; i < array.length; i++) {
let current = array[i]; // 这里相当于a与b交换值所用到的c
while (i - 1 >= 0 && array[i - 1] > current) {
array[i] = array[i - 1];
i--;
}
array[i] = current;
}
return array;
}
# 选择排序
首先将最小的元素存放在序列的起始位置,再从剩余未排序元素中继续寻找最小元素,然后放到已排序的序列后面
该排序是表现最稳定的排序算法之一,因为无论什么数据进去都是 O(n 平方) 的时间复杂度,所以用到它的时候,数据规模越小越好
var a = [1, 3, 6, 3, 23, 76, 1, 34, 222, 6, 456, 221];
function selectSort(array) {
let temp;
let minIndex;
for (let i = 0; i < array.length - 1; i++) {
minIndex = i;
for (let j = i + 1; j < array.length; j++) {
if (array[j] <= array[minIndex]) {
minIndex = j;
}
}
temp = array[i];
array[i] = array[minIndex];
array[minIndex] = temp;
}
return array;
}
console.log(selectSort(a));
# 堆排序
堆排序是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质,即子结点的键值或索引总是小于(或者大于)它的父节点。堆的底层实际上就是一棵完全二叉树,可以用数组实现。
根节点最大的堆叫作大根堆,根节点最小的堆叫作小根堆,你可以根据从大到小排序或者从小到大来排序,分别建立对应的堆就可以
var a = [1, 3, 6, 3, 23, 76, 1, 34, 222, 6, 456, 221];
function heap_sort(array) {
function swap(i, j) {
var temp = array[i];
array[i] = array[j];
array[j] = temp;
}
function max_heapify(start, end) {
var dad = start;
var son = dad * 2 + 1;
if (son >= end) return;
if (son + 1 < end && array[son] < array[son + 1]) {
son++;
}
if (array[dad] <= array[son]) {
swap(dad, son);
max_heapify(son, end);
}
}
for (var i = Math.floor(array.length / 2) - 1; i >= 0; i--) {
max_heapify(i, array.length);
}
for (var j = array.length - 1; j > 0; j--) {
swap(0, j);
max_heapify(0, j);
}
return array;
}
console.log(heap_sort(a));
从代码来看,堆排序相比上面几种排序整体上会复杂一些,不太容易理解。不过你应该知道两点:一是堆排序最核心的点就在于排序前先建堆;二是由于堆其实就是完全二叉树,如果父节点的序号为 n,那么叶子节点的序号就分别是 2n 和 2n+1。
你理解了这两点,再看代码就比较好理解了。堆排序最后有两个循环:第一个是处理父节点的顺序;第二个循环则是根据父节点和叶子节点的大小对比,进行堆的调整。通过这两轮循环的调整,最后堆排序完成。
# 归并排序
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并
var a = [1, 3, 6, 3, 23, 76, 1, 34, 222, 6, 456, 221];
function mergeSort(array) {
const merge = (right, left) => {
const result = [];
let il = 0;
let ir = 0;
while (il < left.length && ir < right.length) {
if (left[il] < right[ir]) {
result.push(left[il++]);
} else {
result.push(right[ir++]);
}
}
while (il < left.length) {
result.push(left[il++]);
}
while (ir < right.length) {
result.push(right[ir++]);
}
return result;
};
const mergeSort = (array) => {
if (array.length === 1) {
return array;
}
const mid = Math.floor(array.length / 2);
const left = array.slice(0, mid);
const right = array.slice(mid, array.length);
return merge(mergeSort(left), mergeSort(right));
};
return mergeSort(array);
}
mergeSort(a);
从 mergeSort 方法中看到,通过 mid 可以把该数组分成左右两个数组,分别对这两个进行递归调用排序方法,最后将两个数组按照顺序归并起来。
归并排序是一种稳定的排序方法,和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好得多,因为始终都是 O(nlogn) 的时间复杂度。而代价是需要额外的内存空间
# sort 实现
先将元素转换为字符串,然后再进行排序 源码 (opens new window)
当 n<=10 时,采用插入排序;
当 n>10 时,采用三路快速排序;
10<n <=1000,采用中位数作为哨兵元素;
n>1000,每隔 200~215 个元素挑出一个元素,放到一个新数组中,然后对它排序,找到中间位置的数,以此作为中位数。
# 为什么元素个数少的时候要采用插入排序
虽然插入排序理论上是平均时间复杂度为 O(n^2) 的算法,快速排序是一个平均 O(nlogn) 级别的算法。但是别忘了,这只是理论上平均的时间复杂度估算,但是它们也有最好的时间复杂度情况,而插入排序在最好的情况下时间复杂度是 O(n)。
在实际情况中两者的算法复杂度前面都会有一个系数,当 n 足够小的时候,快速排序 nlogn 的优势会越来越小。倘若插入排序的 n 足够小,那么就会超过快排。而事实上正是如此,插入排序经过优化以后,对于小数据集的排序会有非常优越的性能,很多时候甚至会超过快排。因此,对于很小的数据量,应用插入排序是一个非常不错的选择
# 为什么要花这么大的力气选择哨兵元素
因为快速排序的性能瓶颈在于递归的深度,最坏的情况是每次的哨兵都是最小元素或者最大元素,那么进行 partition(一边是小于哨兵的元素,另一边是大于哨兵的元素)时,就会有一边是空的。如果这么排下去,递归的层数就达到了 n , 而每一层的复杂度是 O(n),因此快排这时候会退化成 O(n^2) 级别。
这种情况是要尽力避免的,那么如何来避免?就是让哨兵元素尽可能地处于数组的中间位置,让最大或者最小的情况尽可能少。这时候,你就能理解 V8 里面所做的各种优化了。
接下来,我们看一下官方实现的 sort 排序算法的代码基本结构。
function ArraySort(comparefn) {
CHECK_OBJECT_COERCIBLE(this, "Array.prototype.sort");
var array = TO_OBJECT(this);
var length = TO_LENGTH(array.length);
return InnerArraySort(array, length, comparefn);
}
function InnerArraySort(array, length, comparefn) {
// 比较函数未传入
if (!IS_CALLABLE(comparefn)) {
comparefn = function (x, y) {
if (x === y) return 0;
if (% _IsSmi(x) && % _IsSmi(y)) {
return % SmiLexicographicCompare(x, y);
}
x = TO_STRING(x);
y = TO_STRING(y);
if (x == y) return 0;
else return x < y ? -1 : 1;
};
}
function InsertionSort(a, from, to) {
// 插入排序
for (var i = from + 1; i < to; i++) {
var element = a[i];
for (var j = i - 1; j >= from; j--) {
var tmp = a[j];
var order = comparefn(tmp, element);
if (order > 0) {
a[j + 1] = tmp;
} else {
break;
}
}
a[j + 1] = element;
}
}
function GetThirdIndex(a, from, to) { // 元素个数大于1000时寻找哨兵元素
var t_array = new InternalArray();
var increment = 200 + ((to - from) & 15);
var j = 0;
from += 1;
to -= 1;
for (var i = from; i < to; i += increment) {
t_array[j] = [i, a[i]];
j++;
}
t_array.sort(function (a, b) {
return comparefn(a[1], b[1]);
});
var third_index = t_array[t_array.length >> 1][0];
return third_index;
}
function QuickSort(a, from, to) { // 快速排序实现
//哨兵位置
var third_index = 0;
while (true) {
if (to - from <= 10) {
InsertionSort(a, from, to); // 数据量小,使用插入排序,速度较快
return;
}
if (to - from > 1000) {
third_index = GetThirdIndex(a, from, to);
} else {
// 小于1000 直接取中点
third_index = from + ((to - from) >> 1);
}
// 下面开始快排
var v0 = a[from];
var v1 = a[to - 1];
var v2 = a[third_index];
var c01 = comparefn(v0, v1);
if (c01 > 0) {
var tmp = v0;
v0 = v1;
v1 = tmp;
}
var c02 = comparefn(v0, v2);
if (c02 >= 0) {
var tmp = v0;
v0 = v2;
v2 = v1;
v1 = tmp;
} else {
var c12 = comparefn(v1, v2);
if (c12 > 0) {
var tmp = v1;
v1 = v2;
v2 = tmp;
}
}
a[from] = v0;
a[to - 1] = v2;
var pivot = v1;
var low_end = from + 1;
var high_start = to - 1;
a[third_index] = a[low_end];
a[low_end] = pivot;
partition: for (var i = low_end + 1; i < high_start; i++) {
var element = a[i];
var order = comparefn(element, pivot);
if (order < 0) {
a[i] = a[low_end];
a[low_end] = element;
low_end++;
} else if (order > 0) {
do {
high_start--;
if (high_start == i) break partition;
var top_elem = a[high_start];
order = comparefn(top_elem, pivot);
} while (order > 0);
a[i] = a[high_start];
a[high_start] = element;
if (order < 0) {
element = a[i];
a[i] = a[low_end];
a[low_end] = element;
low_end++;
}
}
}
// 快排的核心思路,递归调用快速排序方法
if (to - high_start < low_end - from) {
QuickSort(a, high_start, to);
to = low_end;
} else {
QuickSort(a, from, low_end);
from = high_start;
}
}
}
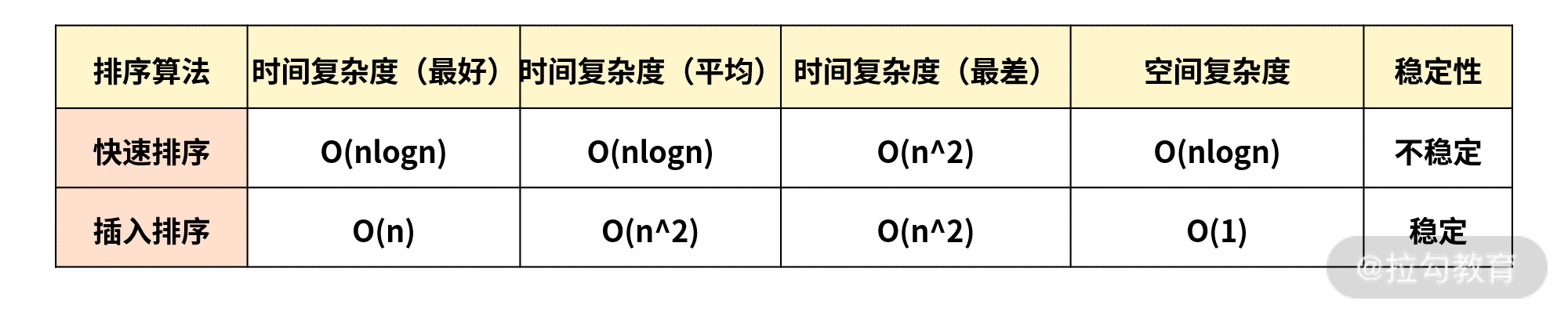
将这两个排序的时间复杂度对比来看,如果当 n 足够小的时候,最好的情况下,插入排序的时间复杂度为 O(n) 要优于快速排序的 O(nlogn),因此就解释了这里当 V8 实现 JS 数组排序算法时,数据量较小的时候会采用插入排序的原因了
# 参考链接